Berechnung des Wärmewiderstands eines Wärmetauschers
Abbildung 1 zeigt eine typische Flüssigkühlschleife mit Kühlplatte (CP), Pumpe und Wärmetauscher (HX), die mit Schläuchen oder Rohren verbunden sind. Da die Bauteile zum Systems gehören, ist es wichtig, sie gleichzeitig auszuwählen, um sicherzustellen, dass sie die richtige Größe für die gewünschte Anwendung haben. Hersteller stellen Leistungsangaben für Kühlplatten und Wärmetauscher üblicherweise separat zur Verfügung. Dabei wird die Leistung von Kühlplatten in Wärmewiderstand und die von Wärmetauschern in Wärmekapazität angegeben. 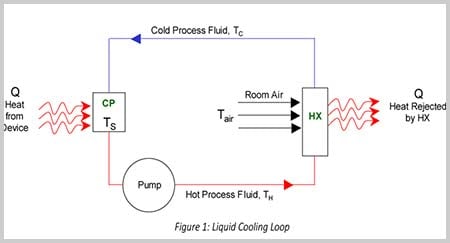Wie wählt man also die besten Wärmetauscher und Kühlplatten für ein komplettes System? Das ist einfacher, als Sie denken. Die Gleichungen für die Bestimmung der richtigen Kombination aus Kühlplatte und Wärmetauscher lassen sich nämlich auf ein sehr einfaches Format reduzieren:
Der erste Schritt, um zu dieser Gleichung zu gelangen, besteht darin, den Wärmewiderstand θCP der Kühlplatte zu berechnen. Dieser ist definiert als der Unterschied zwischen der maximal erforderlichen Oberflächentemperatur, TS, MAX und der Austrittstemperatur der Flüssigkeit TH dividiert durch den gleichmäßig über die gesamte Kühlplattenoberfläche verteilten Wärmestrom Q:
Auf gleiche Weise wird die Wärmekapazität CHX eines Wärmetauschers, die definiert ist als der Wärmestrom Q dividiert durch den Temperaturunterschied zwischen den beiden einfließenden Flüssigkeiten TH - TAIR, von der folgenden Gleichung beschrieben:
Die Wärmekapazität entspricht auch dem Kehrwert des Wärmewiderstands:
Wenn davon ausgegangen wird, dass keine Wärmegewinne von der Pumpe oder Wärmeverluste durch die verbindenden Schläuche und Rohre zwischen Kühlplatte und Wärmetauscher entstehen (da diese in der Regel vernachlässigbar sind), können die Gleichungen (2), (3) und (4) in eine einfache Gleichung vereint werden:
Die Temperatur der Prozessflüssigkeit TH ist nicht länger Teil der Formel, da die Flüssigkeitstemperatur aus der Gleichung entfernt wurde. Durchflussraten und Wärmekapazität der Flüssigkeit müssen nicht berechnet werden. Es verbleiben nur die gewünschte Oberflächentemperatur der Kühlplatte sowie die Temperatur der Umgebungsluft, die den Wärmetauscher kühlt. Die Leistung hängt vollständig vom Wärmewiderstand der Kühlplatte und des Wärmetauschers ab. Somit müssen wir nicht weiter die einzelnen Bauteile des Systems analysieren. Stattdessen bestimmen wir den Wärmewiderstand des gesamten Systems. Beachten Sie bitte, dass der Effekt des Durchstroms nicht aus dem Ergebnis entfernt wurde, da er bereits Teil der Wärmewiderstandvariablen ist.
Ein Kunde möchte eine Kühlplatte CP12 von 12 Zoll (30,48 cm) Seitenlänge nutzen, um 1200 W Wärme von einem elektronischen Gerät mit den Maßen 12 x 5 Zoll (30,48 x 12,70 cm) abzuführen. Als Kühlmittel kommt Wasser mit 1 gpm (3.785 l/min) zum Einsatz, die Raumtemperatur beträgt 20 °C. Der Kunde wünscht den kleinsten Wärmetauscher, der die von diesem Gerät generierte 1200 W Wärme abführen kann und dabei eine maximale Oberflächentemperatur von 80 °C beibehält.
Schritt 1: Zunächst bestimmen wir den Wärmewiderstand, θSYSTEM:
Schritt 2: Jegliche Kombinationen aus Kühlplatte und Wärmetauscher, die einen Wärmewiderstand gleich oder geringer der Systemanforderungen aufweisen, können genutzt werden. Anders ausgedrückt:
Schritt 3: Tabelle 1 zeigt den Widerstand und die Durchflussraten der Kühlplatte CP12 sowie zwei verschiedener Kombinationen von Wärmetauscher und Lüfter:
| Durchflussrate (gpm) | θCP (CP12) (°C/W) | θHX (6110 mit Kona-Lüfter) (°C/W) | θHX (6210 mit Marin-Lüfter) (°C/W) |
| 0,5 | 0,01 | 0,05 | 0,02 |
| 1 | 0,01 | 0,05 | 0,02 |
| 1,5 | 0,01 | 0,04 | 0,02 |
| 1,5 | 0,01 | 0,04 | 0,02 |
| 2 | 0,01 | 0,04 | 0,02 |
Table 1 shows that the CP12/6110 combination satisfies the 0,05 °C/W condition at 2 gpm (0,01 +0,04 = 0.048.
Wenn wir das System als Ganzes betrachten, sehen wir Austauschbeziehungen zwischen verschiedenen Bauteilen, beispielsweise wie sich die Durchflussrate auf die Wahl des Wärmetauschers auswirkt. Bei niedrigen Durchflussraten nimmt der Wärmewiderstand der Kühlplatte zu. Dadurch wird ein größerer Wärmetauscher mit höherer Wärmekapazität und somit niedrigerem Wärmewiderstand erforderlich. Bei höheren Durchflussraten kann ein kleinerer Wärmetauscher verwendet werden.
Flüssigkeit-Luft-Wärmetauscher und Kühlplatten werden oft in Flüssigkeitskreisläufen verwendet. Es ist also wichtig, zu verstehen, wie man die Bauteile gleichzeitig auswählt, um die Systemleistung zu optimieren. Mit genauen Spezifikationen und einer vereinfachten Gleichung kann es aber recht einfach sein, die Bauteile für Ihre Flüssigkeitskühlschleife zu wählen. Darüber hinaus können Sie, wenn Sie Bauteile des gleichen Anbieters verwenden, Komponenten einsetzen, die auf ähnliche Weise getestet wurden und bei denen somit die Wahrscheinlichkeit höher ist, dass sie in einem System gut zusammenarbeiten.
Thermische Berechnungen zur Schrankkühlung
Berechnung des erforderlichen Thermalwiderstands für einen Schrank oder ein Gehäuse
Die Hersteller von Wärmetauschern präsentieren in der Regel thermische Leistungsdaten in Abhängigkeit der Wärmebelastung und den einströmenden Luft- und Wassermengen. Dies funktioniert gut für Anwendungen, bei denen der Wärmetauscher zur Kühlung von Wasser mit Luft verwendet wird, da Sie einfach Ihre Wärmelast. Geben Sie einfach die Lufttemperatur und Flüssigkeitstemperatur ein, um festzustellen, ob er über ausreichend thermische Leistung verfügt.
Bei Schrankkühlanwendungen wird der Wärmetauscher in der umgekehrten Konfiguration verwendet: Kaltes Wasser fließt in den Flüssigkeitskreislauf und warme Luft aus dem Schrank wird beim Durchströmen der Wärmetauscher-Lamellen gekühlt. Bei Anwendungen als Schrankkühlung müssen Sie normalerweise die Temperatur der Luft beim Eintritt in den Schrank und die maximale Temperatur, die die Luft im Schrank erreichen wird, kennen. Beides kann nicht direkt aus den Leistungskurven der Wärmetauscher abgelesen werden.
Der übliche Weg, die Temperaturänderung der Luft zu berechnen, ist die Berechnung des Massenstroms.
Dies kann zeitaufwendig und fehlerbehaftet sein.
To avoid these calculations, Boyd developed charts to quickly estimate temperature rise in common heat transfer media at various heat loads. Diagramme sind für Luft, Wasser, Öl und 30/70-Ethylenglykol-Wasser (EGW) verfügbar. Um die Temperaturänderung zu berechnen, wählen Sie einfach die entsprechende Grafik aus, sehen Sie sich Ihre Durchflussrate und Wärmebelastung an und lesen Sie die Temperaturänderung ab. In our technical library under thermal reference you can view a pdf or our temperature change graphs.
In Verbindung mit Produktleistungskurven bieten diese eine schnelle und einfache Möglichkeit, die Temperatur der in den Schrank eintretenden Kaltluft und die maximale Lufttemperatur im Schrank zu berechnen.
Beispiel für eine Schrankkühlungsberechnung
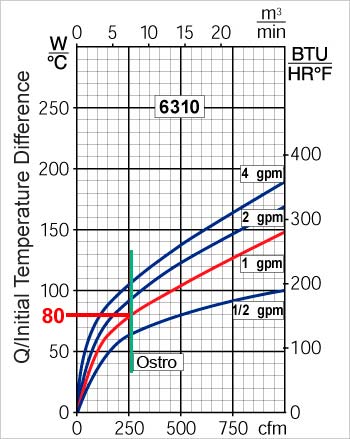
Sie evaluieren den Wärmetauscher 6310 mit einem Ostro-Lüfter zur Kühlung eines Elektronikschranks. Das in den Wärmetauscher eintretende Wasser hat eine Temperatur von 20 °C und eine Durchflussrate von 1 gpm. Die Hitzeladung, Q, ist 2400 W.
Wie hoch ist die Temperatur der gekühlten Luft, die in den Schrank eintritt (d. h. die Temperatur der Luft, die den Wärmetauscher verlässt) und wie hoch ist die maximale Temperatur im Schrank (d. h. die Temperatur der warmen Luft, die in den Wärmetauscher eintritt)?
Überprüfen Sie zunächst die Leistungskurve von 6310 im Katalog. Sie werden sehen, dass bei einem Wasserfluss von 1 gpm und dem Ostro-Lüfter, der ungefähr 250 cfm liefert, seine Leistung 80 W/°C beträgt.
Da wir wissen, dass Q gleich 2400 W und Q/ITD gleich 80 °C/W ist, können wir die Anfangstemperaturdifferenz (ITD) berechnen.
ITD = 2400 W ÷ 80 °C/W = 30 °C
Wir wissen auch, dass die Temperatur des einströmenden Wassers 20 °C beträgt. Wir können daher die Temperatur der einströmenden Luft berechnen:
Temperatur der einströmenden Luft = 20 °C + 30 °C = 50 °C.
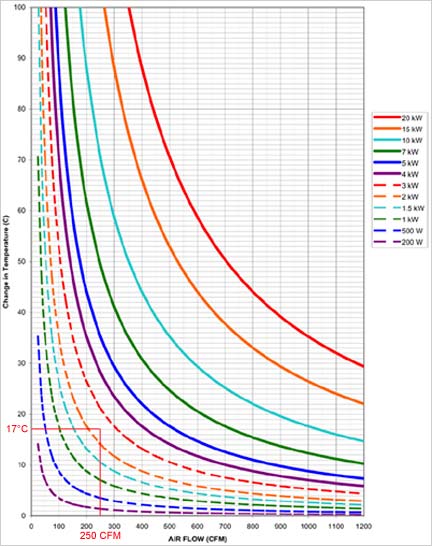
Um die Austrittstemperatur der Luft zu bestimmen, verwenden wir das Diagramm „Air Flow“ (Luftströmung) mit den Parametern 250 CFM und 2400 W.
Wir stellen fest, dass die Temperaturänderung ungefähr 17 °C beträgt. Die Temperatur der Abluft beträgt 50 °C - 17 °C = 33 °C.
Wir wissen, dass dieser Wärmetauscher mit dem Ostro-Lüfter die Luft auf 33 °C abkühlt, und die heißeste Temperatur der Luft im Schrank wird 50 °C erreichen.
Zur Bestimmung der Austrittstemperatur des Wassers verwenden wir das Diagramm „Water Flow“ (Wasserfluss).
Bei 1 gpm und 2400 W zeigt dies, dass die Temperaturänderung ungefähr 9 °C beträgt. Daher beträgt die Temperatur des austretenden Wassers 20 °C + 9 °C = 29 °C.
Diagramme für Luft, Wasser, Öl und EGW stehen im PDF-Format zum Herunterladen zur Verfügung. Diese sind hilfreich für die Dimensionierung von Wärmetauschern und Kühlplatten und sind auch bei einer Vielzahl anderer Temperaturänderungsberechnungen nützlich.
